- Analyzing a mechanism to produce a certain output
- Solving the problem inversely to get the required inputs for achieving the desired outputs
- Results of analysis could be used for designing the system: in Analysis of Mechanisms, for example, finding an unknown length of a link to produce a desired output when given a certain input
- Types of Analysis of Mechanisms
- Positional analysis
- Velocity Analysis
- Acceleration analysis
Chapter 1 included an intro to the analysis of mechanisms based on the understanding of mechanisms
- Modeling and Analysis is a replacement to manufacturing the system then trying experimentally
- Analysis is about finding the relation between inputs and outputs then using this relation to make predictions
- This relation exists due to constraints within system components
- In order to find this relation, we need to a model to express the constraints of the system
- This model (which is just an expression of the constraints of the system) can be mathematical, graphical, etc.
- The mathematical model is just an expression of the constraints of the system in terms of mathematical equations or expressions
- The relation can then be expressed mathematically or as a map between finite inputs and outputs
- Computer programs (software, libraries, etc.) could be used to solve these relations to get the desired predictions
- In case of Positional Analysis, outputs are positions of system components
- In case of analysis of Four-bar mechanism, positional analysis is finding the relation between input angle of a link and output angles of other links
- Constraints in the four-bar mechanism are the lengths of links and types of pairs
- Drawing (Graphically representing the constraints of the system) and intersecting links at a certain point ⇒ Graphical solution
- Writing a math equation (Mathematically representing the constraints of the system) and using the given input ⇒ Mathematical solution
- Graphical Analysis - Graphical Position Analysis
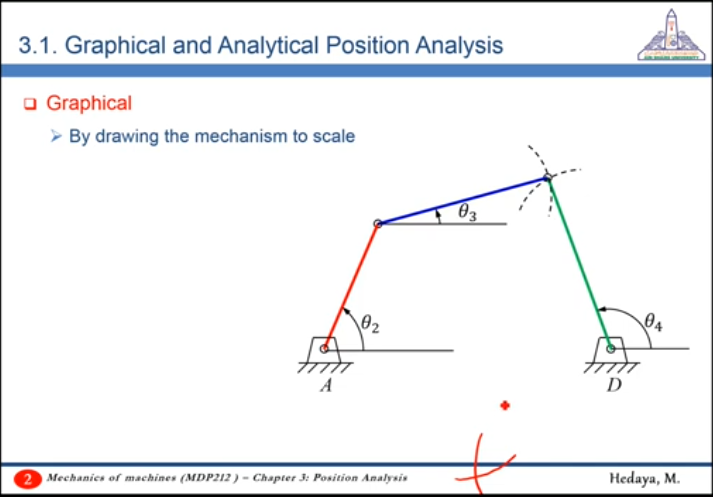
There could be two solutions, the valid solution depends on the assembly of the mechanism
- Analytical Analysis - Analytical Position Analysis
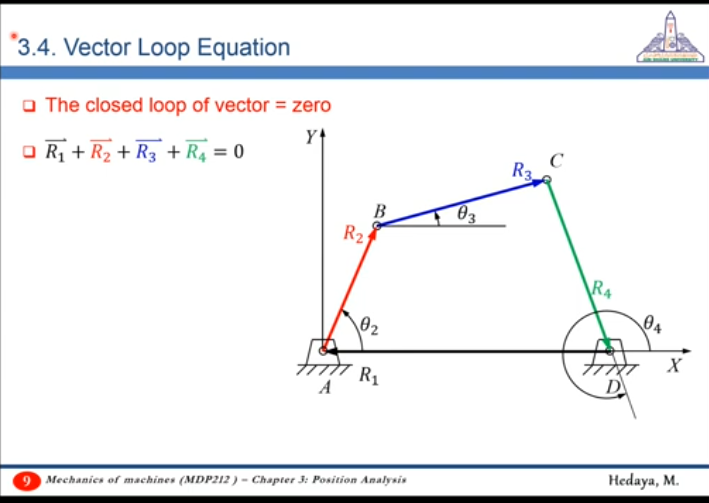
- Loop equation
Design and Analysis are about finding unknowns and making predictions. These unknowns can be
Inputs
System (Mechanism) parameters
Outputs
Analysis is about predicting required input to satisfy desired output given system parameters OR predicting output of a certain input given system parameters. It is like a function of system parameters and either required inputs or desired outputs
Design is about identifying system parameters that satisfy desired outputs given allowable inputs
Examples:
- Problem 1.9 in Sheet 1 requires the length of a link (system parameters) to achieve a desired Quick-return ratio (output), then it asks about the stroke length (output of system given that the input leads to extreme positions)
- Note: some special inputs (like those that lead to special outputs such as angular displacement of rocker) and outputs (like those that the system was designed to achieve such as stroke length or quick return ratio) can be considered among system parameters as well.
- Problem 1.7 in Sheet 1 requires the angular displacements of the crank (input) that leads to the Extreme positions of the block (output)
- Position: using a vector to describe where a point is located
- Displacement: using a vector to describe the change in position of a point
- Motion: using a relation to describe the displacement of points on a rigid body
- Translational Motion: all points on a rigid body have the same displacement vector
- Rotational Motion: one point on a rigid body has displacement of zero and other points non-zero displacements
- General Plane Motion: all points on rigid body translate then rotate or vise versa
18:58 Cartesian and polar co-ordinates could be expressed using complex numbers and Euler form
- Can be arranged to give a better expression of the system
- Can solve for 2 unknowns in plane and for 3 unknowns in space
It's not clever to just write the final equation by doing some trig; the given systems are trivial. You can use that just to check. The goal is being able to model a system, even if it is complex, using mathematical equations. This is the skill that you should train.
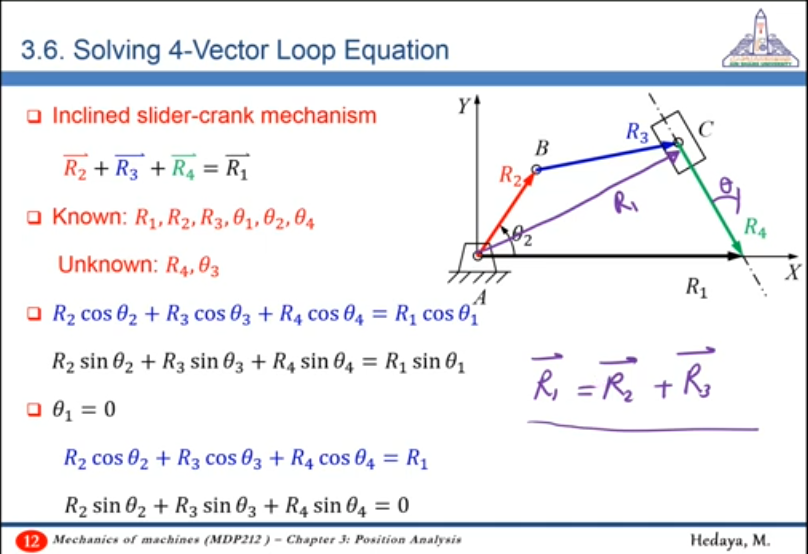
- More than one solution could be obtained; reject solutions that do not express your system, assembly of mechanism in case of Analysis of Mechanisms
- In Analysis of Mechanisms:
- Finding outputs given inputs and dimensions
- Finding dimensions given inputs and desired outputs
- Vector Loop Equation should represent the system to make use of the knowns in the system
- Use Complex Numbers to solve non-linear equations in s
Why does this work?
Complex number give two equations, one for real part and another for imaginary. This property can be applied by using the complex equation and its conjugate to solver for the unknown complex numbers
59:40 Solved example 1 - Analytical Position Analysis on Quick-return mechanism - Crank-shaper mechanism using Vector Loop Equation
- Use complex mode to avoid solving for x and y directions
01:07:18 Solved example 2 - Analytical Position Analysis on Four-bar mechanism using Vector Loop Equation
- Using complex mode to solve for s