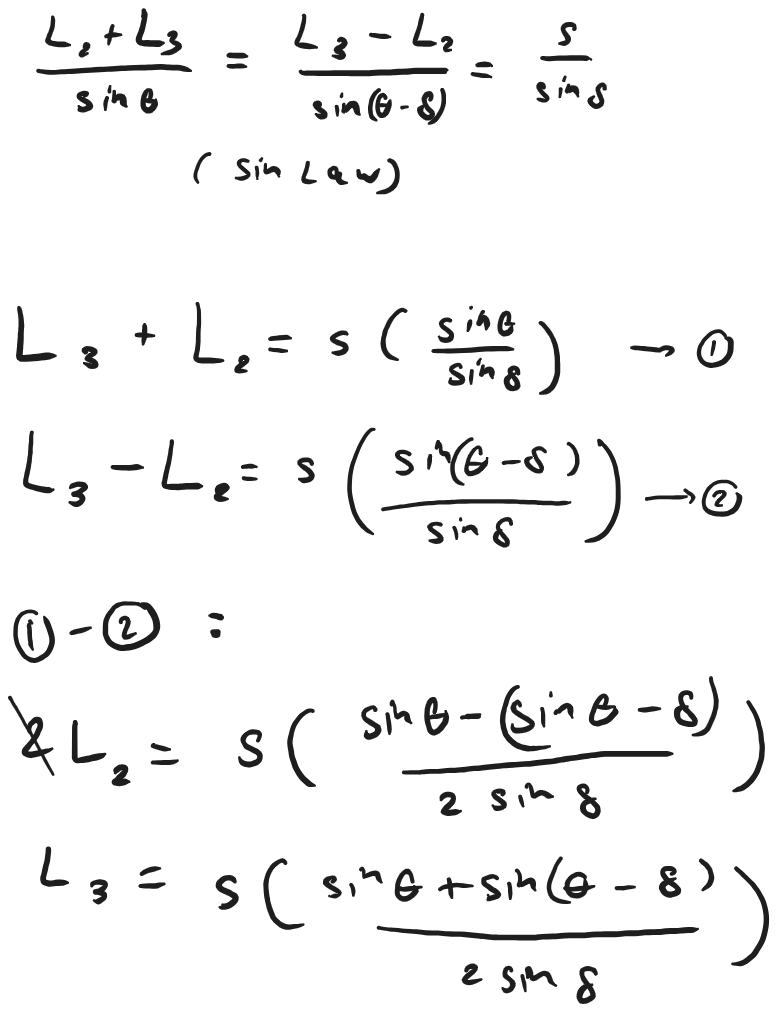πŸ“– ASUPEDIA

Chapter 2.pdf - Google Drive

4 min read

Open Original
Open Original

%200%300%400%Chapter 2Graphical Synthesis of Mechanisms A s s o c . P r o f . Mohamm show annotation

Synthesis of Mechanisms

Methods of Mechanisms Synthesis

00%125%150%200%300%400%Chapter 2 Graphical Synthesis of Mechanisms A s s o c . P r o f . Mohamm show annotation

Graphical Synthesis of Mechanisms

ntM D P 2 1 2 Hedaya, M.22.1. Types of Synthesis of Mechanisms ❑ Function generationThe correla show annotation

Types of Synthesis of Mechanisms

pes of Synthesis of Mechanisms❑ Function generation The correlation of an input moti show annotation

Function generation

nd shipboard gun aiming system❑ Path generation The control of a point in the pl show annotation

Path generation

ya, M.32.1. Types of Synthesis❑ Motion generation The control of a line in the pl show annotation

Motion generation

sition SynthesisHedaya, M.42.2. Extreme positions ❑ 4 bar mechanismM e c h a n i c show annotation

Extreme positions

ons2.3.2.2. Three Positions2.3. Synthesis of four-bar mechanism M e c h a n i c s o f M a c show annotation

Synthesis of four-bar mechanism

a n i s m sHedaya, M.92.3.1.1. Rocker-output, equal time for go and return ❑ Angular displacementM e c h a show annotation

Rocker-output, equal time for go and return - Angular Displacement

a n i s m sHedaya, M.122.3.1.1. Rocker-output, equal time for go and return (cont.)❑ Complex motionM e c h show annotation

Rocker-output, equal time for go and return - Complex motion

a n i s m sHedaya, M.162.3.1.2. Rocker-output, quick return ❑ Angular displacementM e c h a show annotation

Rocker-output, quick return

a n i s m sHedaya, M.192.3.2.1. Coupler-output (two positions) ❑ Complex motionM e c h a n i c show annotation

Coupler-output (two positions)

a n i s m sHedaya, M.222.3.2.2. Coupler-output, three positions ❑ Complex motion (Three Position show annotation

Coupler-output, three positions

OOQQO1 Q1O2Q2O3Q3OO2OO32.3.2.3. Coupler-output, three positions, predefined ground OO1QQ1Hedaya, M.26 M e c h a n i show annotation

Coupler-output, three positions, predefined ground

in position 3.Hedaya, M.282.4. Consideration of 4-bar Mechanism Design ❑ Grashof’s Condition should be show annotation

Consideration of 4-bar Mechanism Design

𝒅+𝒂 πŸπŸπ’ƒπ’„Hedaya, M.312.5. Design of Slider-crank Mechanisms ❑ Many applications require a ma show annotation

Design of Slider-crank Mechanisms

h a n i s m sHedaya, M.322.5.1. In-Line Slider-Crank Mechanism ❑ Stroke, Ξ”π‘ΉπŸ’ π‘šπ‘Žπ‘₯, is the show annotation

In-Line Slider-Crank Mechanism

  • Extreme positions coincide on each other similar to Four-bar mechanism

  • Equal time for go and return

  • Radius of rank obtained from required stroke

h a n i s m sHedaya, M.332.5.2. Offset Slider-Crank Mechanism ❑ Offset distance, 𝐿1, is the d show annotation

Offset Slider-Crank Mechanism

  • Similar to Four-bar mechanism

  • Ratio between go and return

  • Radius of crank obtained from extreme positions

Offset Slider-Crank Mechanism❑ Design of a slider-crank mechanism (Analytically) ➒𝐿1 = 𝐿3 +𝐿2 sin πœƒβˆ’π›Ώ , 𝐿2+ show annotation

Design of a slider-crank mechanism (Analytically)

c h a n i s m sHedaya, M.432.6. Synthesize the crank-shaper mechanism M e c h a n i c s o f M a c show annotation

Synthesis of the crank-shaper mechanism

in the Offset Slider-Crank Mechanism, it was still a Slider-crank mechanism inversion, not the Crank-shaper mechanism inversion

Here, is larger than by only one

c h a n i s m sHedaya, M.472.7. Analytical procedure to synthesize the crank-shaper mechanism ➒𝐿3 = 𝑆2sin 𝛿2➒𝐿2 =𝐿1sin οΏ½ show annotation

Analytical procedure to synthesize the crank-shaper mechanism

Offset Slider-Crank Mechanism❑ The stroke of an offset slider-crank mechanism is always greater than twice the crank length ❑ The feasible range for the off show annotation

Why?

er than twice the crank length❑ The feasible range for th e offset distance➒𝐿1 <𝐿3 βˆ’πΏ2M show annotation

What is this?

Graph View