00%125%150%200%300%400%Chapter 1 Mechanisms A s s t . P r o f . Mohammed show annotation
1 2Hedaya, M.21.1. Definitions❑ Reference frame The coordinates frame considered show annotation
ame considered as a reference.❑ Ground The link which is fixed (no-movi show annotation
utomobile chassis of a crane).❑ Link A rigid body, which is the prima show annotation
rimary element of a mechanism.❑ Kinematic pair (pair)A joint between links in show annotation
ve motion between these links.❑ Kinematic chain A of links connected through kin show annotation
a, M.31.1. Definitions (cont.)❑ Closed kinematic chain A kinematic chain in which the l show annotation
n which the links form a loop.❑ Mechanism A closed kinematic chain with on show annotation
tic chain with one fixed link.❑ Machine A mechanism used to modify ener show annotation
fy energy or do a useful work.❑ Degrees of freedom (D.O.F.) of a link The number of independent coordi show annotation
a, M.41.1. Definitions (cont.)❑ Degrees of freedom (D.O.F.) of a chain The number of independent coordi show annotation
ne the positions of its links.❑ Crank The link which is pivoted to gro show annotation
d makes a complete revolution.❑ Lever (rocker) The link which is pivoted to gro show annotation
c h a n i s m sHedaya, M.51.2. Kinematic pairs ❑ Types of pairs➢Lower pair◼ The show annotation
Kinematic pairs❑ Types of pairs➢ Lower pair ◼ The kinematic pair enables a r show annotation
c pairs (cont.)❑ Types of pairs➢ Higher pair ◼ The kinematic pair enables a r show annotation
edaya, M.51.2. Kinematic pairs❑ Types of pairs ➢Lower pair◼ The kinematic pair show annotation
.71.2. Kinematic pairs (cont.)❑ Degrees of freedom lost by pairing ➢Lower pair ◼ No. of D.O.F. befo show annotation
c h a n i s m sHedaya, M.101.3. Types of links M e c h a n c i c s o f M a show annotation
c h a n i s m sHedaya, M.111.4. Degrees of freedom of a mechanism ❑ Examples◼D.O.F. before pairing show annotation
freedom of a mechanism (cont.)❑ Grübler Equation N = 3(L-1) -2 Pl – PhL: No. of l show annotation
c h a n i s m sHedaya, M.131.5. Four-bar mechanism ❑ Types of four-bar mechanism➢Do show annotation
Four Bar Chain Mechanism Grashof's Law Inversion Of Four Bar Chain
Link to original
- ==== * show annotation
M e c h a n i s m sInputOutput Coupler FrameHedaya, M.141.5. Four-bar m show annotation
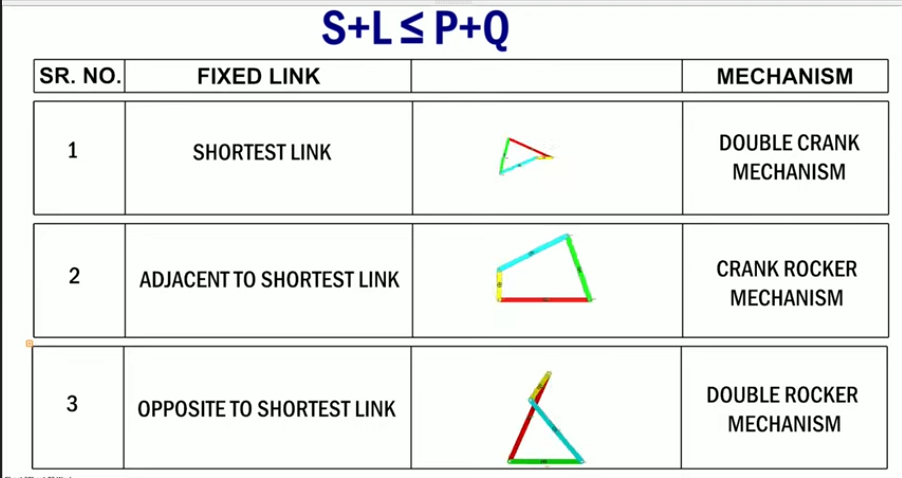
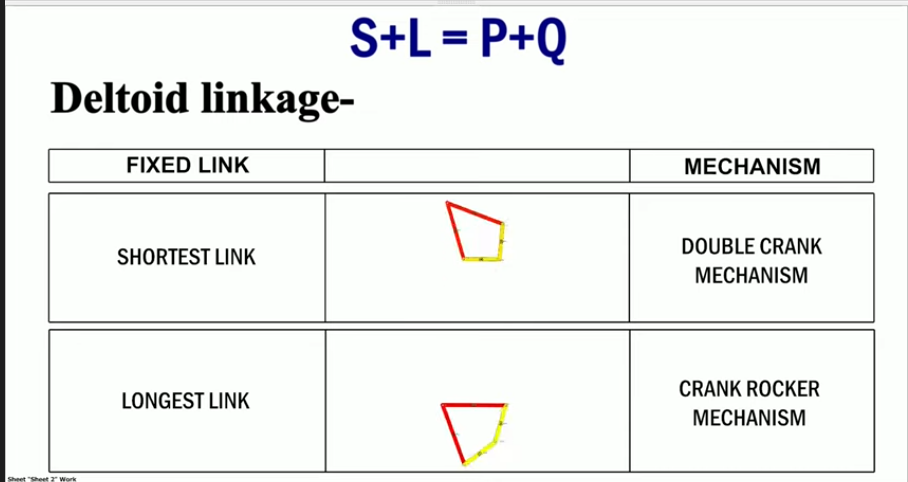
.5. Four-bar mechanism (cont.)❑ Grashof’s condition ➢If S+L > P+Q, the mechanism is show annotation
entM D P 2 1 2Hedaya, M.21.1. Definitions ❑ Reference frameThe coordinates show annotation
e r 1 : M e c h a n i s m s Turning pair xyABCDHedaya, M.81.2. Kinematic show annotation
e r 1 : M e c h a n i s m s Sliding pair xyABCDHedaya, M.91.2. Kinematic show annotation